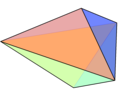
雙三角錐
| 雙三角錐 | |
|---|---|
 (點選檢視旋轉模型) | |
| 類別 | 雙錐 Johnson多面體 J11 - J12 - J13 |
| 面 | 6 |
| 邊 | 9 |
| 頂點 | 5 |
| 歐拉特徵數 | F=6, E=9, V=5 (χ=2) |
| 面的種類 | 三角形 |
| 頂點圖 | V3.4.4 |
| 考克斯特符號 | |
| 對稱群 | D3h, [3,2], (*223) order 12 |
| 對偶 | 三角柱 |
| 旋轉對稱群 | D3, [3,2]+, (223), order 6 |
| 特性 | 凸 |
 | |
 三角柱 (對偶多面體) |  (展開圖) |
在幾何學中,雙三角錐是一種基底為三角形的雙錐體,其為三角柱的對偶。若每個面皆為正三角形,則為92種Johnson多面體(J12)中的其中一個,也是雙角錐的其中一種。顧名思義,它可由正多面體中的兩個大小相同的正四面體組合而成。這92種詹森多面體最早在1996年由詹森·諾曼(Norman Johnson)命名並給予描述。
若不考慮每個面皆為正三角形,只考慮基底為正三角形時,則有可能為廣義的半正多面體的對偶,正三角柱的對偶,此時能使用施萊夫例符號表示,計為 + 3,而在考克斯特符號中,則可以用![]()
![]()
![]()
![]()
![]() 或表示。
或表示。
對偶多面體
雙三角錐的對偶多面體是三角柱,但詹森多面體中所描述的雙三角錐其對偶多面體不是一個正三角柱,是一種五面體由三個矩形和二個三角形組成。
| 雙三角錐的對偶 | 對偶的展開圖 |
|---|---|
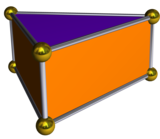 |  |
相關多面體與鑲嵌
雙三角錐可以由三角形二面體透過三角化變換構造而來,因此與三角形二面體具有相同的對稱性,其可以衍生出一些相關的多面體:
對稱群:[3,2], (*322) | [3,2]+, (322) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
 |  |  |  |  | |||||
3,2 | t3,2 | r3,2 | 2t3,2=t2,3 | 2r3,2=2,3 | rr3,2 | tr3,2 | sr3,2 | ||
| 半正對偶 | |||||||||
 |  |  |  |  |  |  |  | ||
V32 | V62 | V32 | V4.4.3 | V23 | V4.4.3 | V4.4.6 | V3.3.3.3 | ||
2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ... | ∞ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
 |  |  |  |  |  | |||||||
| 作为球面镶嵌 | ||||||||||||
 |  |  |  |  |  |  |  |  | ||||
參見
- 詹森多面體
正多面體(柏拉圖立體)- 正四面體
| ||||||||||||||||||||||||||