C++ Eigen for solving linear systems fast
up vote
4
down vote
favorite
So I wanted to test the speed of C++ vs Matlab for solving a linear system of equations. For this purpose I create a random system and measure the time required to solve it using Eigen on Visual Studio:
#include <Eigen/Core>
#include <Eigen/Dense>
#include <chrono>
using namespace Eigen;
using namespace std;
int main()
chrono::steady_clock sc; // create an object of `steady_clock` class
int n;
n = 5000;
MatrixXf m = MatrixXf::Random(n, n);
VectorXf b = VectorXf::Random(n);
auto start = sc.now(); // start timer
VectorXf x = m.lu().solve(b);
auto end = sc.now();
// measure time span between start & end
auto time_span = static_cast<chrono::duration<double>>(end - start);
cout << "Operation took: " << time_span.count() << " seconds !!!";
Solving this 5000 x 5000 system takes 6.4 seconds on average. Doing the same in Matlab takes 0.9 seconds. The matlab code is as follows:
a = rand(5000); b = rand(5000,1);
tic
x = ab;
toc
According to this flowchart of the backslash operator:
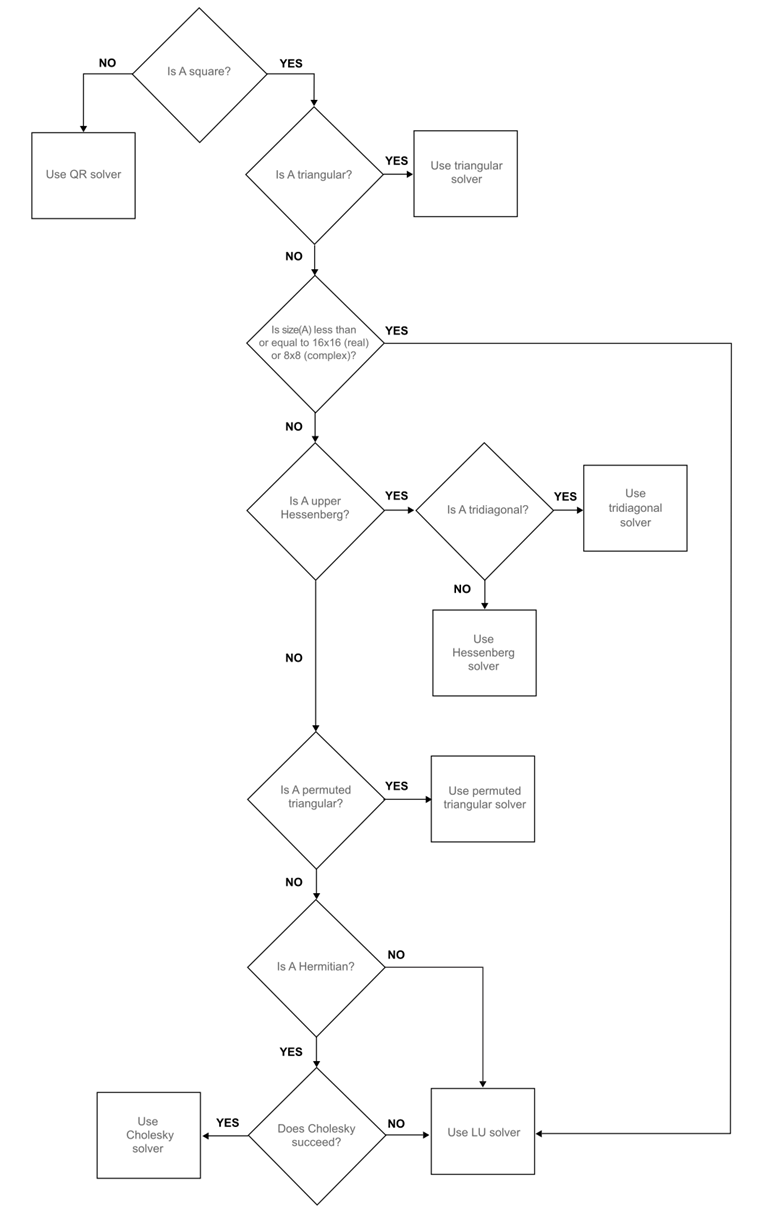
given that a random matrix is not triangular, permuted triangular, hermitian or upper heisenberg, the backslash operator in Matlab uses a LU solver, which I believe is the same solver that I'm using on the C++ code, that is, lu().solve
Probably there is something that I'm missing, because I thought C++ was faster.
- I am running it with release mode active on the Configuration Manager
- Project Properties - C/C++ - Optimization - /O2 is active
- Tried using Enhanced Instructions (SSE and SSE2). SSE actually made it slower and SSE2 barely made any difference.
- I am using Community version of Visual Studio, if that makes any difference
c++ visual-studio matlab benchmarking eigen
|
show 8 more comments
up vote
4
down vote
favorite
So I wanted to test the speed of C++ vs Matlab for solving a linear system of equations. For this purpose I create a random system and measure the time required to solve it using Eigen on Visual Studio:
#include <Eigen/Core>
#include <Eigen/Dense>
#include <chrono>
using namespace Eigen;
using namespace std;
int main()
chrono::steady_clock sc; // create an object of `steady_clock` class
int n;
n = 5000;
MatrixXf m = MatrixXf::Random(n, n);
VectorXf b = VectorXf::Random(n);
auto start = sc.now(); // start timer
VectorXf x = m.lu().solve(b);
auto end = sc.now();
// measure time span between start & end
auto time_span = static_cast<chrono::duration<double>>(end - start);
cout << "Operation took: " << time_span.count() << " seconds !!!";
Solving this 5000 x 5000 system takes 6.4 seconds on average. Doing the same in Matlab takes 0.9 seconds. The matlab code is as follows:
a = rand(5000); b = rand(5000,1);
tic
x = ab;
toc
According to this flowchart of the backslash operator:

given that a random matrix is not triangular, permuted triangular, hermitian or upper heisenberg, the backslash operator in Matlab uses a LU solver, which I believe is the same solver that I'm using on the C++ code, that is, lu().solve
Probably there is something that I'm missing, because I thought C++ was faster.
- I am running it with release mode active on the Configuration Manager
- Project Properties - C/C++ - Optimization - /O2 is active
- Tried using Enhanced Instructions (SSE and SSE2). SSE actually made it slower and SSE2 barely made any difference.
- I am using Community version of Visual Studio, if that makes any difference
c++ visual-studio matlab benchmarking eigen
Can you share your matlab code?
– Lakshay Garg
Nov 11 at 8:42
When I run your code on my machine, it takes 3.18 sec with -O3. I changedm.lu().solve(b);tom.llt().solve(b);and now it takes 0.1sec.
– Lakshay Garg
Nov 11 at 8:48
To be fair, isn't Matlab using double-precision by default, whereas your matrices are single precision? You might want to replace MatrixXf by MatrixXd and VectorXf by VectorXd, right?
– Rulle
Nov 11 at 9:09
2
@Lakshay Garg If I'm not mistaken, llt().solve() uses the Cholesky decomposition LL' to solve the linear system, which should only be valid if the system matrix "m" is positive definite. Given that the matrix is random, this doesn't seem valid.
– user3199900
Nov 11 at 9:10
1
Are you building 32-bit code? If so, why? 64-bit mode has twice as many SIMD registers available, and SSE2 is already the baseline.
– Peter Cordes
Nov 11 at 13:06
|
show 8 more comments
up vote
4
down vote
favorite
up vote
4
down vote
favorite
So I wanted to test the speed of C++ vs Matlab for solving a linear system of equations. For this purpose I create a random system and measure the time required to solve it using Eigen on Visual Studio:
#include <Eigen/Core>
#include <Eigen/Dense>
#include <chrono>
using namespace Eigen;
using namespace std;
int main()
chrono::steady_clock sc; // create an object of `steady_clock` class
int n;
n = 5000;
MatrixXf m = MatrixXf::Random(n, n);
VectorXf b = VectorXf::Random(n);
auto start = sc.now(); // start timer
VectorXf x = m.lu().solve(b);
auto end = sc.now();
// measure time span between start & end
auto time_span = static_cast<chrono::duration<double>>(end - start);
cout << "Operation took: " << time_span.count() << " seconds !!!";
Solving this 5000 x 5000 system takes 6.4 seconds on average. Doing the same in Matlab takes 0.9 seconds. The matlab code is as follows:
a = rand(5000); b = rand(5000,1);
tic
x = ab;
toc
According to this flowchart of the backslash operator:

given that a random matrix is not triangular, permuted triangular, hermitian or upper heisenberg, the backslash operator in Matlab uses a LU solver, which I believe is the same solver that I'm using on the C++ code, that is, lu().solve
Probably there is something that I'm missing, because I thought C++ was faster.
- I am running it with release mode active on the Configuration Manager
- Project Properties - C/C++ - Optimization - /O2 is active
- Tried using Enhanced Instructions (SSE and SSE2). SSE actually made it slower and SSE2 barely made any difference.
- I am using Community version of Visual Studio, if that makes any difference
c++ visual-studio matlab benchmarking eigen
So I wanted to test the speed of C++ vs Matlab for solving a linear system of equations. For this purpose I create a random system and measure the time required to solve it using Eigen on Visual Studio:
#include <Eigen/Core>
#include <Eigen/Dense>
#include <chrono>
using namespace Eigen;
using namespace std;
int main()
chrono::steady_clock sc; // create an object of `steady_clock` class
int n;
n = 5000;
MatrixXf m = MatrixXf::Random(n, n);
VectorXf b = VectorXf::Random(n);
auto start = sc.now(); // start timer
VectorXf x = m.lu().solve(b);
auto end = sc.now();
// measure time span between start & end
auto time_span = static_cast<chrono::duration<double>>(end - start);
cout << "Operation took: " << time_span.count() << " seconds !!!";
Solving this 5000 x 5000 system takes 6.4 seconds on average. Doing the same in Matlab takes 0.9 seconds. The matlab code is as follows:
a = rand(5000); b = rand(5000,1);
tic
x = ab;
toc
According to this flowchart of the backslash operator:

given that a random matrix is not triangular, permuted triangular, hermitian or upper heisenberg, the backslash operator in Matlab uses a LU solver, which I believe is the same solver that I'm using on the C++ code, that is, lu().solve
Probably there is something that I'm missing, because I thought C++ was faster.
- I am running it with release mode active on the Configuration Manager
- Project Properties - C/C++ - Optimization - /O2 is active
- Tried using Enhanced Instructions (SSE and SSE2). SSE actually made it slower and SSE2 barely made any difference.
- I am using Community version of Visual Studio, if that makes any difference
c++ visual-studio matlab benchmarking eigen
c++ visual-studio matlab benchmarking eigen
edited Nov 11 at 12:48
Tân Nguyễn
1
1
asked Nov 11 at 8:37
user3199900
434
434
Can you share your matlab code?
– Lakshay Garg
Nov 11 at 8:42
When I run your code on my machine, it takes 3.18 sec with -O3. I changedm.lu().solve(b);tom.llt().solve(b);and now it takes 0.1sec.
– Lakshay Garg
Nov 11 at 8:48
To be fair, isn't Matlab using double-precision by default, whereas your matrices are single precision? You might want to replace MatrixXf by MatrixXd and VectorXf by VectorXd, right?
– Rulle
Nov 11 at 9:09
2
@Lakshay Garg If I'm not mistaken, llt().solve() uses the Cholesky decomposition LL' to solve the linear system, which should only be valid if the system matrix "m" is positive definite. Given that the matrix is random, this doesn't seem valid.
– user3199900
Nov 11 at 9:10
1
Are you building 32-bit code? If so, why? 64-bit mode has twice as many SIMD registers available, and SSE2 is already the baseline.
– Peter Cordes
Nov 11 at 13:06
|
show 8 more comments
Can you share your matlab code?
– Lakshay Garg
Nov 11 at 8:42
When I run your code on my machine, it takes 3.18 sec with -O3. I changedm.lu().solve(b);tom.llt().solve(b);and now it takes 0.1sec.
– Lakshay Garg
Nov 11 at 8:48
To be fair, isn't Matlab using double-precision by default, whereas your matrices are single precision? You might want to replace MatrixXf by MatrixXd and VectorXf by VectorXd, right?
– Rulle
Nov 11 at 9:09
2
@Lakshay Garg If I'm not mistaken, llt().solve() uses the Cholesky decomposition LL' to solve the linear system, which should only be valid if the system matrix "m" is positive definite. Given that the matrix is random, this doesn't seem valid.
– user3199900
Nov 11 at 9:10
1
Are you building 32-bit code? If so, why? 64-bit mode has twice as many SIMD registers available, and SSE2 is already the baseline.
– Peter Cordes
Nov 11 at 13:06
Can you share your matlab code?
– Lakshay Garg
Nov 11 at 8:42
Can you share your matlab code?
– Lakshay Garg
Nov 11 at 8:42
When I run your code on my machine, it takes 3.18 sec with -O3. I changed
m.lu().solve(b); to m.llt().solve(b); and now it takes 0.1sec.– Lakshay Garg
Nov 11 at 8:48
When I run your code on my machine, it takes 3.18 sec with -O3. I changed
m.lu().solve(b); to m.llt().solve(b); and now it takes 0.1sec.– Lakshay Garg
Nov 11 at 8:48
To be fair, isn't Matlab using double-precision by default, whereas your matrices are single precision? You might want to replace MatrixXf by MatrixXd and VectorXf by VectorXd, right?
– Rulle
Nov 11 at 9:09
To be fair, isn't Matlab using double-precision by default, whereas your matrices are single precision? You might want to replace MatrixXf by MatrixXd and VectorXf by VectorXd, right?
– Rulle
Nov 11 at 9:09
2
2
@Lakshay Garg If I'm not mistaken, llt().solve() uses the Cholesky decomposition LL' to solve the linear system, which should only be valid if the system matrix "m" is positive definite. Given that the matrix is random, this doesn't seem valid.
– user3199900
Nov 11 at 9:10
@Lakshay Garg If I'm not mistaken, llt().solve() uses the Cholesky decomposition LL' to solve the linear system, which should only be valid if the system matrix "m" is positive definite. Given that the matrix is random, this doesn't seem valid.
– user3199900
Nov 11 at 9:10
1
1
Are you building 32-bit code? If so, why? 64-bit mode has twice as many SIMD registers available, and SSE2 is already the baseline.
– Peter Cordes
Nov 11 at 13:06
Are you building 32-bit code? If so, why? 64-bit mode has twice as many SIMD registers available, and SSE2 is already the baseline.
– Peter Cordes
Nov 11 at 13:06
|
show 8 more comments
1 Answer
1
active
oldest
votes
up vote
4
down vote
accepted
First of all, for this kind of operations Eigen is very unlikely to beat MatLab because the later will directly call Intel's MKL which is heavily optimized and multi-threaded. Note that you can also configure Eigen to fallback to MKL, see how. If you do so, you'll end up with similar performance.
Nonetheless, 6.4s is way to much. The Eigen's documentation reports 0.7s for factorizing a 4k x 4k matrix. Running your example on my computer (Haswell laptop @2.6GHz) I got 1.6s (clang 7, -O3 -march=native), and 1s with multithreading enabled (-fopenmp). So make sure you enable all your CPU's feature (AVX, FMA) and openmp. With OpenMP you might need to explicitly reduce the number of openmp threads to the number of physical cores.
The OP only mentions enabling SSE2 (so probably compiling 32-bit code, otherwise SSE2 is baseline) so that also hurts, and tells us they weren't using AVX or FMA. And they're using MSVC which doesn't have any kind of-march=nativeequivalent. As far as I know, with that compiler you have to manually enable stuff your CPU supports because it's only designed for making binaries you distribute, not for local use only. (As well as typically optimizing less well than clang or gcc).
– Peter Cordes
Nov 11 at 13:27
The OP mentions no difference by explicitly enabling SSE2, so I guess it's already compiling 64-bit code.
– ggael
Nov 11 at 13:40
I've read that MSVC doesn't even show you the option for SSE2 in 64-bit mode, you can't disable it. They do say that disabling it by setting only SSE made it slower, and I don't think MSVC will let you do that in 64-bit mode. So probably the default for 32-bit already included SSE2.
– Peter Cordes
Nov 11 at 13:52
By activating AVX, OpenMP and building a 64-bit code instead of using the x86 setting, the time required decreased from 6.4s to 1.4s, far more reasonable. I'll try to use gcc and see if I can improve the time. Thanks!
– user3199900
Nov 13 at 6:20
1.4s is indeed better. Don't miss FMA, this should give you an additional x1.5 speed-up. With MSVC I think you need to enable/arch:AVX2to get FMA.
– ggael
Nov 14 at 12:11
add a comment |
1 Answer
1
active
oldest
votes
1 Answer
1
active
oldest
votes
active
oldest
votes
active
oldest
votes
up vote
4
down vote
accepted
First of all, for this kind of operations Eigen is very unlikely to beat MatLab because the later will directly call Intel's MKL which is heavily optimized and multi-threaded. Note that you can also configure Eigen to fallback to MKL, see how. If you do so, you'll end up with similar performance.
Nonetheless, 6.4s is way to much. The Eigen's documentation reports 0.7s for factorizing a 4k x 4k matrix. Running your example on my computer (Haswell laptop @2.6GHz) I got 1.6s (clang 7, -O3 -march=native), and 1s with multithreading enabled (-fopenmp). So make sure you enable all your CPU's feature (AVX, FMA) and openmp. With OpenMP you might need to explicitly reduce the number of openmp threads to the number of physical cores.
The OP only mentions enabling SSE2 (so probably compiling 32-bit code, otherwise SSE2 is baseline) so that also hurts, and tells us they weren't using AVX or FMA. And they're using MSVC which doesn't have any kind of-march=nativeequivalent. As far as I know, with that compiler you have to manually enable stuff your CPU supports because it's only designed for making binaries you distribute, not for local use only. (As well as typically optimizing less well than clang or gcc).
– Peter Cordes
Nov 11 at 13:27
The OP mentions no difference by explicitly enabling SSE2, so I guess it's already compiling 64-bit code.
– ggael
Nov 11 at 13:40
I've read that MSVC doesn't even show you the option for SSE2 in 64-bit mode, you can't disable it. They do say that disabling it by setting only SSE made it slower, and I don't think MSVC will let you do that in 64-bit mode. So probably the default for 32-bit already included SSE2.
– Peter Cordes
Nov 11 at 13:52
By activating AVX, OpenMP and building a 64-bit code instead of using the x86 setting, the time required decreased from 6.4s to 1.4s, far more reasonable. I'll try to use gcc and see if I can improve the time. Thanks!
– user3199900
Nov 13 at 6:20
1.4s is indeed better. Don't miss FMA, this should give you an additional x1.5 speed-up. With MSVC I think you need to enable/arch:AVX2to get FMA.
– ggael
Nov 14 at 12:11
add a comment |
up vote
4
down vote
accepted
First of all, for this kind of operations Eigen is very unlikely to beat MatLab because the later will directly call Intel's MKL which is heavily optimized and multi-threaded. Note that you can also configure Eigen to fallback to MKL, see how. If you do so, you'll end up with similar performance.
Nonetheless, 6.4s is way to much. The Eigen's documentation reports 0.7s for factorizing a 4k x 4k matrix. Running your example on my computer (Haswell laptop @2.6GHz) I got 1.6s (clang 7, -O3 -march=native), and 1s with multithreading enabled (-fopenmp). So make sure you enable all your CPU's feature (AVX, FMA) and openmp. With OpenMP you might need to explicitly reduce the number of openmp threads to the number of physical cores.
The OP only mentions enabling SSE2 (so probably compiling 32-bit code, otherwise SSE2 is baseline) so that also hurts, and tells us they weren't using AVX or FMA. And they're using MSVC which doesn't have any kind of-march=nativeequivalent. As far as I know, with that compiler you have to manually enable stuff your CPU supports because it's only designed for making binaries you distribute, not for local use only. (As well as typically optimizing less well than clang or gcc).
– Peter Cordes
Nov 11 at 13:27
The OP mentions no difference by explicitly enabling SSE2, so I guess it's already compiling 64-bit code.
– ggael
Nov 11 at 13:40
I've read that MSVC doesn't even show you the option for SSE2 in 64-bit mode, you can't disable it. They do say that disabling it by setting only SSE made it slower, and I don't think MSVC will let you do that in 64-bit mode. So probably the default for 32-bit already included SSE2.
– Peter Cordes
Nov 11 at 13:52
By activating AVX, OpenMP and building a 64-bit code instead of using the x86 setting, the time required decreased from 6.4s to 1.4s, far more reasonable. I'll try to use gcc and see if I can improve the time. Thanks!
– user3199900
Nov 13 at 6:20
1.4s is indeed better. Don't miss FMA, this should give you an additional x1.5 speed-up. With MSVC I think you need to enable/arch:AVX2to get FMA.
– ggael
Nov 14 at 12:11
add a comment |
up vote
4
down vote
accepted
up vote
4
down vote
accepted
First of all, for this kind of operations Eigen is very unlikely to beat MatLab because the later will directly call Intel's MKL which is heavily optimized and multi-threaded. Note that you can also configure Eigen to fallback to MKL, see how. If you do so, you'll end up with similar performance.
Nonetheless, 6.4s is way to much. The Eigen's documentation reports 0.7s for factorizing a 4k x 4k matrix. Running your example on my computer (Haswell laptop @2.6GHz) I got 1.6s (clang 7, -O3 -march=native), and 1s with multithreading enabled (-fopenmp). So make sure you enable all your CPU's feature (AVX, FMA) and openmp. With OpenMP you might need to explicitly reduce the number of openmp threads to the number of physical cores.
First of all, for this kind of operations Eigen is very unlikely to beat MatLab because the later will directly call Intel's MKL which is heavily optimized and multi-threaded. Note that you can also configure Eigen to fallback to MKL, see how. If you do so, you'll end up with similar performance.
Nonetheless, 6.4s is way to much. The Eigen's documentation reports 0.7s for factorizing a 4k x 4k matrix. Running your example on my computer (Haswell laptop @2.6GHz) I got 1.6s (clang 7, -O3 -march=native), and 1s with multithreading enabled (-fopenmp). So make sure you enable all your CPU's feature (AVX, FMA) and openmp. With OpenMP you might need to explicitly reduce the number of openmp threads to the number of physical cores.
answered Nov 11 at 13:15
ggael
19.8k22944
19.8k22944
The OP only mentions enabling SSE2 (so probably compiling 32-bit code, otherwise SSE2 is baseline) so that also hurts, and tells us they weren't using AVX or FMA. And they're using MSVC which doesn't have any kind of-march=nativeequivalent. As far as I know, with that compiler you have to manually enable stuff your CPU supports because it's only designed for making binaries you distribute, not for local use only. (As well as typically optimizing less well than clang or gcc).
– Peter Cordes
Nov 11 at 13:27
The OP mentions no difference by explicitly enabling SSE2, so I guess it's already compiling 64-bit code.
– ggael
Nov 11 at 13:40
I've read that MSVC doesn't even show you the option for SSE2 in 64-bit mode, you can't disable it. They do say that disabling it by setting only SSE made it slower, and I don't think MSVC will let you do that in 64-bit mode. So probably the default for 32-bit already included SSE2.
– Peter Cordes
Nov 11 at 13:52
By activating AVX, OpenMP and building a 64-bit code instead of using the x86 setting, the time required decreased from 6.4s to 1.4s, far more reasonable. I'll try to use gcc and see if I can improve the time. Thanks!
– user3199900
Nov 13 at 6:20
1.4s is indeed better. Don't miss FMA, this should give you an additional x1.5 speed-up. With MSVC I think you need to enable/arch:AVX2to get FMA.
– ggael
Nov 14 at 12:11
add a comment |
The OP only mentions enabling SSE2 (so probably compiling 32-bit code, otherwise SSE2 is baseline) so that also hurts, and tells us they weren't using AVX or FMA. And they're using MSVC which doesn't have any kind of-march=nativeequivalent. As far as I know, with that compiler you have to manually enable stuff your CPU supports because it's only designed for making binaries you distribute, not for local use only. (As well as typically optimizing less well than clang or gcc).
– Peter Cordes
Nov 11 at 13:27
The OP mentions no difference by explicitly enabling SSE2, so I guess it's already compiling 64-bit code.
– ggael
Nov 11 at 13:40
I've read that MSVC doesn't even show you the option for SSE2 in 64-bit mode, you can't disable it. They do say that disabling it by setting only SSE made it slower, and I don't think MSVC will let you do that in 64-bit mode. So probably the default for 32-bit already included SSE2.
– Peter Cordes
Nov 11 at 13:52
By activating AVX, OpenMP and building a 64-bit code instead of using the x86 setting, the time required decreased from 6.4s to 1.4s, far more reasonable. I'll try to use gcc and see if I can improve the time. Thanks!
– user3199900
Nov 13 at 6:20
1.4s is indeed better. Don't miss FMA, this should give you an additional x1.5 speed-up. With MSVC I think you need to enable/arch:AVX2to get FMA.
– ggael
Nov 14 at 12:11
The OP only mentions enabling SSE2 (so probably compiling 32-bit code, otherwise SSE2 is baseline) so that also hurts, and tells us they weren't using AVX or FMA. And they're using MSVC which doesn't have any kind of
-march=native equivalent. As far as I know, with that compiler you have to manually enable stuff your CPU supports because it's only designed for making binaries you distribute, not for local use only. (As well as typically optimizing less well than clang or gcc).– Peter Cordes
Nov 11 at 13:27
The OP only mentions enabling SSE2 (so probably compiling 32-bit code, otherwise SSE2 is baseline) so that also hurts, and tells us they weren't using AVX or FMA. And they're using MSVC which doesn't have any kind of
-march=native equivalent. As far as I know, with that compiler you have to manually enable stuff your CPU supports because it's only designed for making binaries you distribute, not for local use only. (As well as typically optimizing less well than clang or gcc).– Peter Cordes
Nov 11 at 13:27
The OP mentions no difference by explicitly enabling SSE2, so I guess it's already compiling 64-bit code.
– ggael
Nov 11 at 13:40
The OP mentions no difference by explicitly enabling SSE2, so I guess it's already compiling 64-bit code.
– ggael
Nov 11 at 13:40
I've read that MSVC doesn't even show you the option for SSE2 in 64-bit mode, you can't disable it. They do say that disabling it by setting only SSE made it slower, and I don't think MSVC will let you do that in 64-bit mode. So probably the default for 32-bit already included SSE2.
– Peter Cordes
Nov 11 at 13:52
I've read that MSVC doesn't even show you the option for SSE2 in 64-bit mode, you can't disable it. They do say that disabling it by setting only SSE made it slower, and I don't think MSVC will let you do that in 64-bit mode. So probably the default for 32-bit already included SSE2.
– Peter Cordes
Nov 11 at 13:52
By activating AVX, OpenMP and building a 64-bit code instead of using the x86 setting, the time required decreased from 6.4s to 1.4s, far more reasonable. I'll try to use gcc and see if I can improve the time. Thanks!
– user3199900
Nov 13 at 6:20
By activating AVX, OpenMP and building a 64-bit code instead of using the x86 setting, the time required decreased from 6.4s to 1.4s, far more reasonable. I'll try to use gcc and see if I can improve the time. Thanks!
– user3199900
Nov 13 at 6:20
1.4s is indeed better. Don't miss FMA, this should give you an additional x1.5 speed-up. With MSVC I think you need to enable
/arch:AVX2 to get FMA.– ggael
Nov 14 at 12:11
1.4s is indeed better. Don't miss FMA, this should give you an additional x1.5 speed-up. With MSVC I think you need to enable
/arch:AVX2 to get FMA.– ggael
Nov 14 at 12:11
add a comment |
Thanks for contributing an answer to Stack Overflow!
- Please be sure to answer the question. Provide details and share your research!
But avoid …
- Asking for help, clarification, or responding to other answers.
- Making statements based on opinion; back them up with references or personal experience.
To learn more, see our tips on writing great answers.
Some of your past answers have not been well-received, and you're in danger of being blocked from answering.
Please pay close attention to the following guidance:
- Please be sure to answer the question. Provide details and share your research!
But avoid …
- Asking for help, clarification, or responding to other answers.
- Making statements based on opinion; back them up with references or personal experience.
To learn more, see our tips on writing great answers.
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
StackExchange.ready(
function ()
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fstackoverflow.com%2fquestions%2f53247078%2fc-eigen-for-solving-linear-systems-fast%23new-answer', 'question_page');
);
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Can you share your matlab code?
– Lakshay Garg
Nov 11 at 8:42
When I run your code on my machine, it takes 3.18 sec with -O3. I changed
m.lu().solve(b);tom.llt().solve(b);and now it takes 0.1sec.– Lakshay Garg
Nov 11 at 8:48
To be fair, isn't Matlab using double-precision by default, whereas your matrices are single precision? You might want to replace MatrixXf by MatrixXd and VectorXf by VectorXd, right?
– Rulle
Nov 11 at 9:09
2
@Lakshay Garg If I'm not mistaken, llt().solve() uses the Cholesky decomposition LL' to solve the linear system, which should only be valid if the system matrix "m" is positive definite. Given that the matrix is random, this doesn't seem valid.
– user3199900
Nov 11 at 9:10
1
Are you building 32-bit code? If so, why? 64-bit mode has twice as many SIMD registers available, and SSE2 is already the baseline.
– Peter Cordes
Nov 11 at 13:06