ローレンツ力
この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。(2016年12月) |
電磁気学 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
 | ||||||||||||
| ||||||||||||
| ||||||||||||
ローレンツ力(ローレンツりょく、英: Lorentz force)は、電磁場中で運動する荷電粒子が受ける力のことである。
名前はヘンドリック・ローレンツに由来する。
目次
1 概要
2 ローレンツ力と仕事
3 ローレンツ力と電磁力
4 相対論的な表示
5 ローレンツ力の向き
6 関連項目
概要
電場 E(t,x)displaystyle boldsymbol E(t,boldsymbol x)




F(t)=qE(t,r(t))+qv(t)×B(t,r(t))displaystyle boldsymbol F(t)=qboldsymbol E(t,boldsymbol r(t))+qboldsymbol v(t)times boldsymbol B(t,boldsymbol r(t))
である。この Fdisplaystyle boldsymbol F
× はクロス積である。
上式で右辺第一項は電場中で荷電粒子が受ける力でありクーロン力とも呼ばれる。
第二項はビオ=サバールの法則を一般化した形となっている。
ここで荷電粒子が加速度運動している(ローレンツ力によっても加速度運動となっている)とすると、その荷電粒子自身による電磁場の効果が存在するが、その影響はごく小さい場合が多いので通常は無視されるか、ごく小さなものとして扱われる。
F=q(v×B)displaystyle boldsymbol mathit F=q(boldsymbol mathit vtimes boldsymbol mathit B)
と近似することができる。
荷電粒子の速度 v と磁場 B のクロス積 がローレンツ力 F であることは、フレミング左手の法則で向きを確認できる。
ローレンツ力と仕事
ローレンツ力のする仕事は
dW=F⋅dr=q(E+v×B)⋅drdisplaystyle beginaligneddW&=boldsymbol Fcdot dboldsymbol r\&=q(boldsymbol E+boldsymbol vtimes boldsymbol B)cdot dboldsymbol r\endaligned
である。
ここで、磁場による力の項は、
dWm=q(v×B)⋅dr=qv⋅(v×B)dt=0displaystyle beginaligneddW_m&=q(boldsymbol vtimes boldsymbol B)cdot dboldsymbol r\&=qboldsymbol vcdot (boldsymbol vtimes boldsymbol B)dt=0\endaligned
であり、磁場は仕事をしない。ここで v = dr/dt を用いた。
電場による力の項は、
dWe=qE⋅dr=qv⋅Edt=wdtdisplaystyle beginaligneddW_e&=qboldsymbol Ecdot dboldsymbol r\&=qboldsymbol vcdot boldsymbol Edt=w,dt\endaligned
である。この電場による仕事量は、巨視的に見るとジュール熱に相当する。
磁場による力は速度と直交する方向に生じるので、運動の向きを変えるだけで粒子の運動エネルギーは変化しない。エネルギーの移動は電場により生じている。
ローレンツ力と電磁力
電荷 qi の時刻 t における位置を ri、速度を viとすると、電荷密度 ρ 、電流密度 j は、
ρ(t,x)=∑iqiδ(x−ri(t))displaystyle rho (t,boldsymbol x)=sum _iq_idelta (boldsymbol x-boldsymbol r_i(t))
j(t,x)=∑iqivi(t)δ(x−ri(t))displaystyle boldsymbol j(t,boldsymbol x)=sum _iq_iboldsymbol v_i(t)delta (boldsymbol x-boldsymbol r_i(t))
と表すことができる。δ(x)はディラックのデルタ関数である。
ローレンツ力は多数の粒子系に対しては
F(t)=∑iqi(E(t,ri(t))+vi(t)×B(t,ri(t)))displaystyle boldsymbol F(t)=sum _iq_ileft(boldsymbol E(t,boldsymbol r_i(t))+boldsymbol v_i(t)times boldsymbol B(t,boldsymbol r_i(t))right)
となる。ここで、
E(t,ri(t))=∫d3xδ(x−ri(t))E(t,x)displaystyle boldsymbol E(t,boldsymbol r_i(t))=int !!d^3x,delta (boldsymbol x-boldsymbol r_i(t))boldsymbol E(t,boldsymbol x)
B(t,ri(t))=∫d3xδ(x−ri(t))B(t,x)displaystyle boldsymbol B(t,boldsymbol r_i(t))=int !!d^3x,delta (boldsymbol x-boldsymbol r_i(t))boldsymbol B(t,boldsymbol x)
として、和と積分を入れ替えると、
F(t)=∫d3x(ρ(t,x)E(t,x)+j(t,x)×B(t,x))displaystyle boldsymbol F(t)=int !!d^3x,left(rho (t,boldsymbol x)boldsymbol E(t,boldsymbol x)+boldsymbol j(t,boldsymbol x)times boldsymbol B(t,boldsymbol x)right)
このようにミクロな粒子に作用する力(ローレンツ力)から、マクロな粒子系に作用する力(クーロン力及びアンペール力)が導かれた。
相対論的な表示
ローレンツ力を相対論的に記述すると
p˙μ=qz˙νFνμ(z)displaystyle dot p_mu =qdot z^nu F_nu mu (z)
となる。
ここで z=(ct,r) は粒子の相対論的な位置、p=(E/c,p) は粒子の相対論的な運動量、ドットは運動のパラメータによる微分である。
F は電場と磁場を合わせた電磁テンソルで、具体的には
(F01,F02,F03)=(E1/c,E2/c,E3/c), (F32,F13,F21)=(B1,B2,B3)displaystyle (F_01,F_02,F_03)=(E_1/c,E_2/c,E_3/c),~(F_32,F_13,F_21)=(B_1,B_2,B_3)
と表される。
位置の微分は非相対論的な速度 v によって
z˙μ=(ct˙,t˙v)displaystyle dot z^mu =(cdot t,dot tboldsymbol v)
と表される。
従って、この式の空間成分は
p˙=qt˙E(t,r)+qt˙v×B(t,r)displaystyle dot boldsymbol p=qdot tboldsymbol E(t,boldsymbol r)+qdot tboldsymbol vtimes boldsymbol B(t,boldsymbol r)
となる。非相対論的な力 f は
f=dpdt=p˙t˙=qE(t,r)+qv×B(t,r)displaystyle boldsymbol f=frac dboldsymbol pdt=frac dot boldsymbol pdot t=qboldsymbol E(t,boldsymbol r)+qboldsymbol vtimes boldsymbol B(t,boldsymbol r)
となる。
ローレンツ力の向き
ローレンツ力:
F=q(v×B)displaystyle boldsymbol mathit F=q(boldsymbol mathit vtimes boldsymbol mathit B)
の向きを示すフレミングの左手の法則がある。
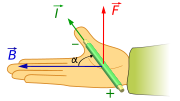
ローレンツ力の向きを表す右手の法則
また、右手の姿で示す方法もある。
関連項目
- マクスウェルの方程式
- フレミング左手の法則
- 電磁気学















