Myujth

電磁気学
電気 磁性
静電気学 電荷 クーロンの法則 電場 電束 ガウスの法則 電位 静電誘導 電気双極子（英語版） 分極電荷密度 静磁気学（英語版） アンペールの法則 電流 磁場 磁化 磁束 ビオ・サバールの法則 磁気モーメント ガウスの法則（英語版） 電気力学（英語版） 自由空間 ローレンツ力 起電力 電磁誘導 ファラデーの法則 レンツの法則 変位電流 マクスウェルの方程式 電磁場（英語版） 電磁波 リエナール・ヴィーヘルト・ポテンシャル（英語版） マクスウェル・テンソル 渦電流 電気回路 電気伝導 電気抵抗 静電容量 インダクタンス インピーダンス リアクタンス アドミタンス サセプタンス 共鳴空洞（英語版） 導波管（英語版） 共変定式（英語版） 電磁テンソル（英語版） 電磁圧力エネルギーテンソル（英語版） 4元電流密度 電磁ポテンシャル 科学者 アンペール クーロン ファラデー ガウス ヘヴィサイド ヘンリー ヘルツ ローレンツ マクスウェル テスラ ボルタ ヴェーバー エルステッド
表・話・編・歴

アンペールの法則（アンペールのほうそく; 英語: Ampère's circuital law）は電流とそのまわりにできる磁場との関係をあらわす法則である。1820年にフランスの物理学者アンドレ＝マリ・アンペール(フランス語: André-Marie Ampère)が発見した。

概要

現在一般に知られているアンペールの法則の記述は次のようなものである。閉じた経路にそって磁場の大きさを足し合わせる。すると、足し合わせた結果は閉じた経路を貫く電流の和に比例する。磁場の足し合わせは線積分でおこなう。

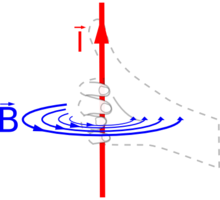
図1: 右手の法則

アンペールは実験で2本の電流のあいだに働く力を観測し、そして実験結果をアンペールの法則にまとめ、それ以前に発見されていた電磁気の現象を説明することに成功した。
アンペールは、電流を流すと、電流の方向を右ネジの進む方向として、右ネジの回る向きに磁場が生じることを発見した。図1のように右手の親指を立てて手を握ると、電流の方向を親指の向きとした時、残りの指の向きが磁界の向きと一致するため右手の法則と呼ばれる。日本では右ねじの法則と呼ばれることも多い。

たとえば、無限に長い直線導線に電流を流す。このとき電流の回りには同心円上で右ねじ方向の磁場が出来る。閉じた経路として半径 r の同心円をとるとその上で磁場の大きさは等しく、これを H とする。アンペールの法則によれば、

2πrH=Idisplaystyle 2pi rH,=I

という関係が成り立つ。ただし I は電流、r は電流との距離。これを変形すると次の直線電流の磁場の公式、

H=I2πrdisplaystyle H=frac I2pi r

が得られる。これはビオ・サバールの法則を積分したものと一致する。

一般式による表現

アンペールの法則は、周回積分・面積分によって一般式で表すと、下記のとおりとなる。

∮∂S⁡H⋅dl=∫SJ⋅dS=Idisplaystyle oint _partial Sboldsymbol Hcdot mathrm d boldsymbol l=int _Sboldsymbol Jcdot mathrm d boldsymbol S=I

ここで、

である。

この式は、ある面 S 内を電流が貫くと、その電流と等しい磁場が面の境界 ∂S で右ねじの法則に従った方向に生じるということを示している。

回転 (rot)による拡張・数学的整備

アンペールの法則はジェームズ・クラーク・マクスウェルにより拡張と数学的整備を加えられて、マクスウェルの方程式の4つの方程式の1つになっている（アンペール-マクスウェルの式）。その正体は磁気におけるガウスの法則である。

電流場のループCの微小変化による周回積分（∮C⁡H⋅dl=Idisplaystyle oint _Cboldsymbol Hcdot dboldsymbol l=I）の変化率をrotH を使い、次式で表す。

(rotH)n=limΔS→01ΔS∮ΔC⁡H⋅dldisplaystyle (boldsymbol mathsf rotboldsymbol H)_n=lim _Delta Sto 0frac 1Delta Soint _Delta Cboldsymbol Hcdot dboldsymbol l

ここでΔCはΔSの境界であり、(rotH)_nとはΔSの法線方向の成分と言う意味である。

これを使うとアンペールの法則は

rotH=Jdisplaystyle boldsymbol mathsf rotboldsymbol H=boldsymbol J

と表すことができる。

rotはrotation（ローテーション）の略で「回転」の意味である。また微分演算子∇(ナブラ)を用いて、

∇×H=Jdisplaystyle nabla times boldsymbol H=boldsymbol J

と書くこともできる。これは前述のとおり、マクスウェルの方程式のひとつである。

参考文献

• 金古喜代治『改訂 電気磁気学』学献社,1983年,ISBN 4-7623-1031-X
  

関連項目

• マクスウェルの方程式


• 回転 (ベクトル解析)


• ビオ・サバールの法則