Myujth

数学の様々な分野において、ある特定の状況下にて一意に射を定めるような抽象的性質が、特定の構成を定義、あるいは特徴づけたりする事がしばしばある。このような性質を普遍性（英: universal property）と呼ぶ。普遍性は圏論を用いて抽象的に論考される。

結果として、我々は普遍性の一般的な扱い方を得ることになる。例えば、群の直積や直和、自由群、積位相, ストーン－チェックのコンパクト化, テンソル積, 逆極限と順極限, 核と余核, 引き戻し, 押し出しおよびイコライザ、など。

（en:universal_property （08:43, 27 October 2005）より翻訳）

形式的定義

U : D → C を圏 D から圏 C への関手とし、X をCの対象とする。X から Uへの普遍射 （universal morphism）は、D の対象 A とCの射 φ : X → U(A) からなる対(A, φ)で表され、かつ以下の普遍性（universal property）を満たす。

Y がDの対象で f : X → U(Y) がCの射であるような場合、常に射 g : A → Yが一意に存在して、次の図を可換にする。

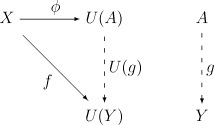
射 g の存在は、直感的には(A, φ)が「十分に一般的」であることを示しながら、一方で射の一意性は、(A, φ)が「過度に一般的ではない」事を表している。

また、上述の定義で全ての射を逆向きにすることで、圏論的な双対を考えることができる。U から X への普遍射は、Dの対象A とCの射 φ : U(A) → X の対(A, φ)で表され、かつ以下の普遍性を満たす。

Y が Dの対象で f : U(Y) → X がCの射であるような場合、常に射g : Y → A が一意に存在して、次の図を可換にする。

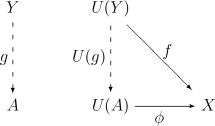
ここで、人によっては一方を普遍射と呼び、もう一方を余普遍射（co-universal property）と呼ぶ場合もある事に注意されたい。どちらがどちらかはその人次第である。

さまざまな普遍性

存在と一意性

数量を定義することがその存在を保障することにはならない。与えられた関手U及び上述の対象Xに対し、X から U （もしくはU から X）の普遍射は、存在するかもしれないし、存在しないかもしれない。しかしながら、もし、普遍射 (A, φ) が存在すれば、一意な同型射を除いて一意的である。すなわち、もし別の対 (A ' , φ ' ) が存在すれば、一意な同型射g : A → A ' が存在して φ ' = U(g)φ となる。これは (A ' , φ ' ) を普遍射の定義にしたがって (Y, f) と置き換えることで容易に確かめられる。

同値な定義

普遍射の定義は様々な方法で置き換えることができる。U を D から C への関手とし、X を C の対象とする。このとき、以下は全て同値である。

(A, φ) は X から U への普遍射である

(A, φ) はコンマ圏 (X ↓ U) の始対象である

(A, φ) は Hom_C(X, U—) の表現である。

これらと双対な以下の定義もまたそれぞれに同値である。

(A, φ) は U から X への普遍射である。

(A, φ) はコンマ圏 (U ↓ X) の終対象である。

(A, φ) は Hom_C(U—, X) の表現である。

随伴関手との関係

(A₁, φ₁) を X₁ から U への普遍射、 (A₂, φ₂) を X₂ から U への普遍射とする。普遍性から、任意の射 h : X₁ → X₂ に対して一意な射 g : A₁ → A₂ が存在して、次の図式を可換にする。

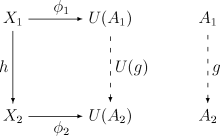
もし 全ての C の対象 X_i にU への普遍射が認められるならば、X_i $mapsto$ A_i 及び h $mapsto$ g によってC から D への関手 Vが定義される。これに伴って、φ_i は 1_C （C の恒等関手）から U V への自然変換を定義する。関手 (V, U) は随伴関手の対となる。（V は U の左随伴、及び U は V の右随伴）

同様の言明は U からの普遍射という双対な状況においても適用できる。全ての C における X について、関手 V : C → D が得られ、これは U への右随伴になっている。（つまり U は V の左随伴である。）

実際、このような方法で全ての随伴関手の対を普遍的構成から得られる。F と G を単位（unit）η と余単位（co-unit）ε （定義は随伴関手の記事を参考のこと）によって構成される随伴関手の対とする。このとき、任意の対象 C と D への普遍射が得られる。

C の各対象 X に対し、 (F(X), η_X) は X から G への普遍射である。つまり、任意の f : X → G(Y) に対して一意な g : F(X) → Y が存在して以下の図式を可換にする。

D の各対象 Y に対し、 (G(Y), ε_Y) は F から Y への普遍射である。つまり、任意の g : F(X) → Y に対して一意な f : X → G(Y) が存在して以下の図式を可換にする。

普遍的構成は随伴関手の対より更に一般的である。普遍的構成は最適化問題のようなものだ。この問題が C 中の全ての対象（同様に、D の全ての対象）について解を持つとき、かつそのときのみ随伴関手の対が得られる。 .

例

ここで、この一般的なアイデアを明らかにすべく3つの有効な例を挙げる。読者は導入部で例示した記事を参照すれば、他にもたくさんの例を構築できるだろう。

テンソル代数

C を体 K 上のベクトル空間の圏 K-Vect とし、 D をK 上の多元環 K-Alg （ユニタリーかつ結合的と仮定）とする。U を、各多元環をその基底となるベクトル空間に写す忘却関手とする。

K上の任意のベクトル空間 V において、V のテンソル代数 T(V) を構成できる。テンソル代数の普遍性は i : V → T(V) が埋め込み写像となるような対 (T(V), i) を表し、これは V から U への普遍射となる。

この構成は任意のベクトル空間 V において有効であり、それゆえ T は K-Vect から K-Alg への関手だと結論付けられる。この関手は忘却関手 U に対して左随伴となる。

核

D を（群の圏のような）ゼロ射を伴う圏とし、 f : X → Y を D の射とする。f の核とは、以下を満たすような任意の射 k: K → X を指す。

f k は K から Y へのゼロ射である。

f k ' がゼロ射であるような任意の射 k ' : K ' → X に対し、一意な射 u: K ' → K が存在して k u = k ' が成り立つ。

これを上述の一般的設定の枠組みにおいて理解するために、D 中の射の圏 C を定義する。C の対象は D の射 f : X → Y とし、f : X → Y から g : S → T への射は射 α : X → S および β : Y → T の対 (α,β) とし、f = gα が成り立つものとする。

ここで、D の対象 K をゼロ射 0_KK : K → K に、射 r : K → L を対 (r,r) に写すような関手 F : D → C を定義する。

すると、圏 Dにおける射 f : X → Y （圏 C における対象）および D における対象K が与えられたとき、F(K) から f への射は f k = l 0_KK = 0_KY となるような対 (k,l) によって与えられる。これはまさしく上述で与えられた普遍射によって映し出されるものそのものである。この抽象的な “F から f への普遍射 ” は核の普遍性以外の何者でもない。

極限と余極限

極限と余極限は普遍的構成のある重要な特殊ケースである。 J および C を小さいJ を伴う圏とする。（J を添字圏とみなす）そして、C^J を対応する関手圏（functor category）とする。対角関手（diagonal functor） Δ : C → C^J は C の各対象 N を、N への定数関手（constant functor） Δ(N) : J → C （つまり、J 中の各 X について Δ(N)(X) = N）に写す関手である。

関手 F : J → C （C^J の対象）が与えられたとき、 F の極限（limit）は、存在すれば、 Δ から F への普遍射に他ならない。この双対として、F の 余極限（colimit）は F から Δ への普遍射に他ならない。

どのようなメリットがあるのか？

もし、ある構成が普遍性によって与えられることがわかれば、そのことで幾つかの利得を得ることができる。

普遍性は同型を除いて一意的な対象を定義する。したがって、2つの対象が同型だと証明する事は、すなわちそれらが同じ普遍性を満たすことを示す事である。

与えられた構成の具体的な中身がぐちゃぐちゃになっていても、その構成が普遍性を満たすならば、それらの中身を見なくてすむ。つまり、その構成について知らなければならない全てのものは既にその普遍性に内包されているのである。もし具体的な詳細でなく普遍性が使われたなら、証明は短くかつエレガントになる事が多い。

もし普遍的構成が全ての C における X に適用できるなら、そこから、C から D への関手を得られる、という事実を知ることができる。. （つまり、例えば、核の形成は関手的（functorial）である。すなわち、射 f から射 g への各射 (α,β) は、f の核から g の核への射を導き出す。）

さらに、この関手は U に対して右もしくは左随伴になる。しかし右随伴は極限と可換になり、左随伴は余極限と可換になる。（すなわち、例えば写像のある直積の核は核の直積と等しくなる事がすぐに結論付けられる。）

歴史

様々な位相幾何学的構成における普遍性は1948年にピエール・サミュエルによって示された。これらは後にブルバキにて拡張された形で用いられた。随伴関手に近い関係を持つ概念はそれ自体独立した形で、1958年にダニエル・カンによって導入された。

参考文献

Cohen, Paul M., Universal Algebra (1981), D.Reidel Publishing, Holland. ISBN 90-277-1213-1.

Mac Lane, Saunders, Categories for the Working Mathematician 2nd ed. (1998), Graduate Texts in Mathematics 5. Springer. ISBN 0-387-98403-8.

搜尋此網誌