脈衝寬度調變

一個例子脈寬調製:供電電壓(藍色)調製為一系列的脈衝產生一個正弦樣磁通密度波形(紅色),在磁路的電磁致動器。平滑的波形由此可以控制的寬度和數目的脈衝調製(每特定週期)
脉冲宽度调制(英语:Pulse Width Modulation,缩写:PWM),简称脉宽调制,是將模拟信號轉換為脈波的一種技術,一般轉換後脈波的週期固定,但脈波的工作週期會依模拟信號的大小而改變。
在模拟电路中,模拟信号的值可以连续进行变化,在时间和值的幅度上都几乎没有限制,基本上可以取任何实数值,输入与输出也呈线性变化。所以在模拟电路中,电压和电流可直接用来进行控制对象,例如家用电器设备中的音量开关控制、采用卤素灯泡灯具的亮度控制等等。
但模拟电路有诸多的问题:例如控制信号容易随时间漂移,难以调节;功耗大;易受噪声和环境干擾等等。
與模拟电路不同,数字电路是在预先确定的范围内取值,在任何时刻,其输出只可能为ON和OFF两种状态,所以电压或电流会通/断方式的重复脉冲序列加载到模拟负载。PWM技术是一种对模拟信号电平的数字编码方法,通过使用高分辨率计数器(调制频率)调制方波的占空比,从而实现对一个模拟信号的电平进行编码。其最大的优点是从处理器到被控对象之间的所有信号都是数字形式的,无需再进行数模转换过程;而且对噪声的抗干扰能力也大大增强(噪声只有在强到足以将逻辑值改变时,才可能对数字信号产生实质的影响),这也是PWM在通讯等信号传输行业得到大量应用的主要原因。
模拟信号能否使用PWM进行编码调制,仅依赖带宽,这即意味着只要有足够的带宽,任何模拟信号值均可以采用PWM技术进行调制编码,一般而言,负载需要的调制频率要高于10Hz,在实际应用中,频率约在1kHz到200kHz之间。
在信号接收端,需将信号解调还原为模拟信号,目前在很多微型控制器(MCU)内部都包含有PWM控制器模块。
目录
1 歷史
2 原理
2.1 微分調變
2.2 积分-微分調變
2.3 空間向量調變
2.4 直接轉矩控制
2.5 時間比例
2.6 類型
2.7 光譜
2.8 脈衝寬度調變的取樣定理
3 應用
3.1 伺服
3.2 電信
3.3 能量的傳遞
4 参见
5 参考文献
6 外部链接
歷史
在過去,當只有部分能量需求(以縫紉機馬達為例),一個變阻器(被放在縫紉機的腳踏板上)串接在一個馬達上將會調整流入馬達中的電流,同時會因為電阻發熱而消耗一些能量。這其實是一個可以接受(因為總能量夠低)但沒有效率的方式。然而,變阻器只是一個控制能量的方法之一(可參考自耦變壓器做為參考),因此一個可以達到較低成本又有效率的調整方法是被需要的。這個機制同時可以被運用來當作電扇馬達、幫浦馬達、機器伺服等,同時必須足夠精細與檯燈系統互動,因此,脈衝寬度調變應運而生,作為這個複雜問題的一個解決方案。
一種早期的脈衝寬度調變方式是辛克萊X10,一個在1960年代的10瓦音樂放大器之套件版本。差不多時期脈衝寬度調變亦開始被應用在交流電馬達控制之上。[1]
而在最近一個世紀中,有些變速的電子馬達已經有很好的效率,但他們相較於等速馬達來說較為複雜,而且有些時候需要較為大型的外部儀器輔助,像是可變電阻及如沃德里奧納多驅動器一樣的(Ward Leonard drive)旋轉器。
原理

圖一: 一個脈衝波, 顯示 ymindisplaystyle y_textmin
 , ymaxdisplaystyle y_textmax
, ymaxdisplaystyle y_textmax 和工作循環D的關係.
和工作循環D的關係.脈衝寬度調變使用一個脈衝寬度會被調變的方波,使得波型的平均值會有所變化。如果我們考慮一個週期為 Tdisplaystyle T



- y¯=1T∫0Tf(t)dt.displaystyle bar y=frac 1Tint _0^Tf(t),dt.
當 f(t)displaystyle f(t)




- y¯=1T(∫0DTymaxdt+∫DTTymindt)=1T(D⋅T⋅ymax+T(1−D)ymin)=D⋅ymax+(1−D)ymin.displaystyle beginalignedbar y&=frac 1Tleft(int _0^DTy_textmax,dt+int _DT^Ty_textmin,dtright)\&=frac 1Tleft(Dcdot Tcdot y_textmax+Tleft(1-Dright)y_textminright)\&=Dcdot y_textmax+left(1-Dright)y_textmin.endaligned
以上表示可以在很多狀況下被簡化,當 ymin=0displaystyle y_textmin=0

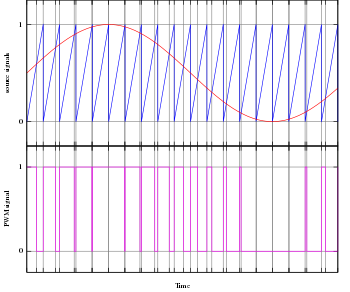
圖二: 一個可以對於給定的訊號簡單產生脈衝寬度調變的方法,收到訊號(紅色線)相比於一個鋸齒波(藍色線),當後者比前者小時,調變後訊號會在高狀態,反之則在低狀態。
最簡單可以產生一個脈衝寬度調變訊號的方式是交集性方法(intersective method),這個方法只需要使用鋸齒波或三角波(可以簡單地使用震盪器來產生),以及一個比較器。當參考的訊號值(圖二的紅色波)比鋸齒波(圖二的藍色波)來的大,則脈衝調變後的結果會在高狀態,反之,則在低狀態。
微分調變
以微分調變作為控制脈衝寬度調變的方法,輸出訊號將會被積分,同時結果也會被拿來與參考訊號增減一個偏移量(作為比較的邊界)比較。當每一次的積分結果到達邊界時,脈衝調變訊號便會轉變狀態如圖三。
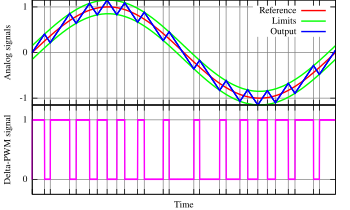
圖三: 微分脈衝寬度調變的原理. 輸出訊號 (藍色) 與邊界做比較 (綠色). 這些邊界是由參考訊號(紅色)增減一個篇偏移量得到。當每一次輸出訊號到達其中一個邊界,脈衝寬度調變訊號便會轉換狀態
积分-微分調變
以积分-微分調變作為控制脈衝寬度調變的方法,參考訊號與輸出訊號會相減得到誤差訊號。 同時此誤差會被積分,若積分超過邊界,輸出結果便會轉換狀態(參考圖四)。

圖四:微分-积分脈衝寬度調變的原理。 上面綠色的波型是參考訊號,輸出訊號(下圖,脈衝寬度調變)會與之相減得到誤差訊號(上圖之藍線)。 此誤差會被積分(中圖),若積分超過邊界(紅線),輸出結果便會轉換狀態。
空間向量調變
空間向量調變是一種針對多相位交流訊號,控制脈衝寬度調變的演算法,先將參考訊號正常的取樣,接著對於每一次的樣本訊號,會有一些在參考向量相鄰的非零交換向量以及一至多個的零交換向量作為取樣之代表,目的是合成出參考向量。
直接轉矩控制
直接轉矩控制是一種控制交流馬達的方式。這個和微分調變方式非常類似(參考上面),馬達的力矩以及磁力線可以被估計,當訊號要偏離磁滯帶時,藉由打開裝置的半導體開關,可以使其被控制在磁滯帶之中。
時間比例
很多數位電路都可以產生出脈衝寬度調變訊號(比方說很多微型控制器可以有很多脈衝寬度調變),正常來說,這些數位電路都會使用一個每隔一段固定時間便會增加1的計數器(直接或不直接連接到電路的時間皆可)並且在脈衝寬度調變訊號的最後會被重置。當這個計數器比參考值來得多的時候,調變訊號的輸出便會轉換狀態。[2] 這個技術被稱為時間比例,特別是時間比例控制[3]。
這個會定時增加的計數器是一個離散版本的相交性方法的鋸齒波。相交性方法的類比比較器將會變成一個在現今的計數值以及數位參考值之間簡單的積分比較。這個工作循環只會在每一次離散的步驟間有所變動,會是一個計數器精細度的函數。然而,一個高精細度的計數器將可以提供令人滿意的表現。
類型
有三種類型的脈衝寬度調變是可能的:
- 脈衝波的中心將會被固定在時間窗格的中心,同時脈衝波的兩邊可以移動,使得波的寬度被延伸或壓縮。
- 脈衝波領先的邊將會被固定在時間窗格領先的邊上,並且針對脈衝波的落後邊進行調變。
- 直接固定脈衝波的落後邊,再針對脈衝波的領先邊進行調變。
光譜
上述這三種類型的調變所產生的光譜是相似的,而且每一種都會包含一個直流的元素,一個基底邊帶在每一個諧波中,會包含調變過後的信號以及相位調變的載波。這些諧波的振幅大小會被限制在一個 sinx/xdisplaystyle sin x/x
反過來說,积分調變是一個可以製造出連續光譜,且不需要連續的諧波之隨機過程。
脈衝寬度調變的取樣定理
脈衝寬度調變的轉換過程是非線性的,且我們一般假設其在低頻濾波的還原上是不完美的。根據脈衝寬度調變的取樣定理,我們可以發現,脈衝寬度調變的轉換可以是完美的。這個定理敘述當 "對於任何有基頻頻帶限制的訊號,若其大小在正負0.637間,可以被單位大小的脈衝寬調變所產生的訊號所代表,波的脈衝數會等於奈奎斯特(Nyquist)取樣的數量,且峰值的限制與波是兩階還是三階互相獨立"。取樣定理告訴我們:一個有頻帶限制的訊號,如果我們的取樣頻率大於傳遞波頻率的兩倍,則訊號傳遞後可以被完整地重建。
應用
伺服
脈衝寬度調變可以用於控制伺服機構。
電信
在電信使用上,脈衝寬度調變是一種訊號調變的形式,其脈衝波的寬度對應到另一個特定資料會在傳送端被編碼,並於接收端解碼。
不同長度的脈衝波(要傳遞的訊息本身)將會每隔固定的時間後被傳遞(載波的頻率)
_ _ _ _ _ _ _ _
| | | | | | | | | | | | | | | |
Clock | | | | | | | | | | | | | | | |
__| |____| |____| |____| |____| |____| |____| |____| |____
_ __ ____ ____ _
PWM signal | | | | | | | | | |
| | | | | | | | | |
_________| |____| |___| |________| |_| |___________
Data 0 1 2 4 0 4 1 0
時間訊號不一定要被包含脈衝寬度調變的傳遞上,事實上資料的領先端可以被當成一個計時器使用,如果有一個小的偏移量被加在資料值之上,去避免資料值有一個長度為零的脈衝波。
_ __ ___ _____ _ _____ __ _
| | | | | | | | | | | | | | | |
PWM signal | | | | | | | | | | | | | | | |
__| |____| |___| |__| |_| |____| |_| |___| |_____
Data 0 1 2 4 0 4 1 0
能量的傳遞
脈衝寬度調變可以被用來控制對於一個載子能量傳遞的多寡,而不會產生由阻抗所造成的線性能量傳遞損失。此方法所需要付出的代價是,載子所流失的能量並非一個常數且是不連續的(如降壓式轉換器),載子上傳遞的能量也不是連續的。然而,由於載子可能是具有高頻電感性的,這時就必須要外加一個被動的電子濾波器,讓這些脈衝波變為平滑且能復原平均的類比波型,能量流入載子才會是連續的。而從供應端流出的能量則不是連續的,因此大部分情況下需要額外的能量儲存空間。(比方說在一個電路下,一個電容會吸收儲存於供應端電感的能量。)
参见
- ΔΣ調變
- 脈衝振幅調變
- 脈衝編碼調變
- 脈衝相位調變
- 空間向量調變
参考文献
^ Schönung, A.; Stemmler, H. Geregelter Drehstrom-Umkehrantrieb mit gesteuertem Umrichter nach dem Unterschwingungsverfahren. BBC Mitteilungen (Brown Boveri et Cie). August 1964, 51 (8/9): 555–577.
^ www.netrino.com – Introduction to Pulse Width Modulation (PWM)
^ Fundamentals of HVAC Control Systems, by Robert McDowall, p. 21
^ Hausmair, Katharina; Shuli Chi; Peter Singerl; Christian Vogel. Aliasing-Free Digital Pulse-Width Modulation for Burst-Mode RF Transmitters. IEEE Transactions on Circuits and Systems I: Regular Papers. February 2013, 60 (2): 415–427. doi:10.1109/TCSI.2012.2215776.
外部链接
维基共享资源中相关的多媒体资源:脈衝寬度調變 |
- Tutorial video on PWM including example motor speed control and LED dimming circuits
- An Introduction to Delta Sigma Converters
- Pulse Width Modulation in PID control loop - free simulator
- Pulse Width Modulation in Desktop monitors - monitor flicker

