Myujth

萊曼系是物理學上氫原子的電子從主量子數n大於等於2躍遷至n = 1的一系列光譜線。這些系列以希臘字母依序標示：n = 2躍遷至n = 1稱為萊曼-α，3躍遷至1稱為萊曼-β，4躍遷至1稱為萊曼-γ，依此類推。這個序列的譜線是以發現者萊曼命名為萊曼系。

歷史

第一條萊曼系的譜線是萊曼在1906年在研究被激發的氫原子氣體紫外線光譜時發現的，其餘的譜線在1906年1914年間陸續被發現。

氫所發出的這些譜線是不連續的，這是氫譜線第一系列的例證：

歷史上，解釋氫光譜是物理學的難題，这些谱线的不连续，出现的位置也无法解释。1855年巴耳末提出巴耳末公式（經驗公式）。芮得柏花了不到5年的時間將經驗公式擴充為芮得柏公式，包含了可见光之外的谱线，原始的公式在1888年提出在1890年完成。芮得柏設法發展了另一個不僅可以和已知的巴耳末系吻合的經驗式，並且能預測其他未知的譜線，將不同的整數置入芮得柏的經驗式可以發現和得到不同的氫光譜系列譜線。

萊曼系

得到萊曼系譜線的芮得柏公式如下：

1λ=R(112−1n2)(R=1.0974×107m−1)displaystyle 1 over lambda =Rleft(1 over 1^2-1 over n^2right)qquad left(R=1.0974times 10^7mboxm^-1right)

此處n是大於或等於2的一個整數（也就是n = 2,3,4,...）。

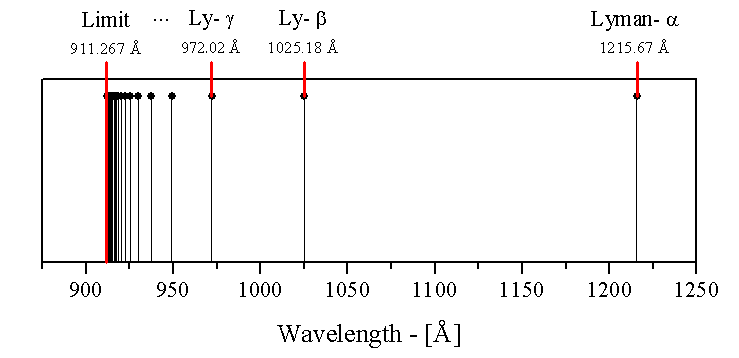
因此，因此在上面圖中譜線的波長從右至左分別對應於n=2displaystyle n=2,至n=∞displaystyle n=infty （對應於無限多條的譜線，n越大，谱线的间距越小，因為图像的精度限制，好像形成了连续谱，但氢光谱都是分离的不连续的谱线。）。

萊曼系的波長都属于紫外波段：

ndisplaystyle n	2	3	4	5	6	7	8	9	10	11	∞displaystyle infty
波長（nm）	121.6	102.5	97.2	94.9	93.7	93.0	92.6	92.3	92.1	91.9	91.15

解釋和推導

在1913年，尼爾斯·波耳提出他的波耳模型理論，說明为何芮得柏公式能夠解釋氫原子的譜線。波耳發現電子氫原子的能階必需以下面的公式所描述的量子化：

En=−me42(4πε0ℏ)21n2=−13.6n2[eV].displaystyle E_n=-me^4 over 2left(4pi varepsilon _0hbar right)^21 over n^2=-13.6 over n^2[mboxeV].

依據波耳的第三個假設，當電子由最初的能階（Eidisplaystyle E_i）躍遷至最後的能階（Efdisplaystyle E_f），原子必需輻射如下波長的輻射：

λ=hcEi−Ef.displaystyle lambda =hc over E_i-E_f.

當以電子伏特表示能量，以埃作為波長的單位時，能夠更方便的表示：

λ=12430Ei−Ef.displaystyle lambda =12430 over E_i-E_f.

在上面的公式中用於表示氫原子時，習慣以n對應於開始時的能階，m對應於結束時的能階：

1λ=Ei−Ef12430=(1243013.6)−1(1m2−1n2)=R(1m2−1n2)displaystyle 1 over lambda =E_i-E_f over 12430=left(12430 over 13.6right)^-1left(1 over m^2-1 over n^2right)=Rleft(1 over m^2-1 over n^2right)

此處的R同樣是芮得柏長久以來就知道的芮得柏常數。

要將波耳、芮得柏和萊曼聯結在一起，只需要將m以1來取代：

1λ=R(112−1n2)displaystyle 1 over lambda =Rleft(1 over 1^2-1 over n^2right)

這就是芮得柏公式的萊曼系。因此，每一條輻射的波長都對應於一種電子從主量子數大於1的能階上躍遷至第一階的能量。

相關條目

• 波耳模型


• H-α


• 芮得柏公式


• 氫原子光譜


• 萊曼連續光子

外部連結

• Lyman series (animation)


• Lyman discovers series

查 论 编 氢原子光谱 光譜系 1:萊曼系 2:巴耳末系 3:帕申系 4:布拉克系 5:蒲芬德系 6:韓福瑞系 关连用语 里德伯常量 里德伯公式 精细结构 超精细结构 蘭姆位移 斯塔克效应 氫原子  · 玻尔模型